Quantum communication
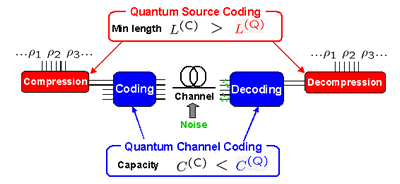
Alphabets from the information source (ρ1, ρ2, ρ3, ...) are first converted into bit sequences by the source encoder so as to compress original messages into smaller bits. Essentially, source coding entails representation of common alphabet in a message as short sequences of bits, and uncommon alphabet as longer sequences, to make the average length of the coded message as short as possible. The unequal frequencies of the letters imply a redundancy that enables the compression of the message. The outputs from the source encoder are further encoded by the channel encoder into appropriate code words by adding some redundant bits to protect information from noise disturbances in the channel. An output from the channel is generally different from an input code word due to noise. Then at the receiving side, we try to decode the original signal by applying appropriate error correction. Finally we decompress the decoded signal to restore the original messages.
Shannon established information theory by quantifying the effectiveness and the limits of these codings in 1948. Shannon's information theory is a quite mathematical and hence very general theory. Unfortunately, however, Shannon's information theory is not perfect modeling of physics behind information. Information theory should eventually be represented by the words of quantum mechanics. It is quite recently, after 90's, when such representations are clarified.
In quantum information theory, alphabets in the above viewgraph ρ1, ρ2, ρ3, ... are now the density matrices representing quantum states of signals. When one considers coding with these quantum states explicitly, one can entails quantum effects to overcome the performances in conventional theory. For example;
(1) In compression process, when the quantum states are non-commuting with each other, then there is another redundancy that does not have any classical counterpart, and further compression is possible even if these quantum alphabets appear with equal frequencies. (Quantum source coding)
(2) Concerning channel coding, one may consider a decoding process assisted by a quantum computation, i.e. a decoding by entangling the letter quantum states prior to the final measurement. One can then attain a higher capacity than the Shannon capacity limit. (Quantum channel coding)
We have been working on how to demonstrate these predicted quantum effect experimentally. Although it is still a formidable task to implement quantum coding by using quantum gates working on practical quantum particles for communications, it is possible to test the basic concepts of quantum information theory with currently available photonic technologies.
(1) Quantum signal detection
We have developed quantum detection circuit working at the single photon level by using linear optics, and have tested its performance using quasi-single photon source, i.e. attenuated laser light and Si-APDs. This technique plays an important role for experimental demonstration of quantum coding.
<Reference>
(2) Quantum source coding
Based on the above technique, we have demonstrated quantum source coding theorem experimentally. As mentioned above, a message consisting of non-commuting quantum states includes the redundancy that has no counterpart in classical information theory. Significantly, compression of such message is possible now even if the prior probabilities for the letters are equal. This additional redundancy comes from the non-commutativity of the alphabets and can be removed by first entangling the quantum letter states appropriately and by then discarding unimportant letter states. In addition to its fundamental role in quantum information theory, the compression of non-commutative data sets has several practical advantages, for example, to save expensive quantum channel resources in quantum cryptographic schemes using non-orthogonal states or in long-haul optical communication channels where signals are extremely attenuated coherent pulses.
Although the original message can be faithfully decompressed in the limit of infinite block length, compression-decompression is associated with finite errors for finite block length. In practice, therefore, we evaluate the parameter called "fidelity" that quantifies how close the reconstructed message and the original one are. In our experiment, a three-qubit message consisting of three non-orthogonal letter states is compressed into a two-qubit signal and then decompressed again. Physically, three qubits are encoded in two linear polarization and four path modes of a quasi-single photon. In the compression process, each letter of this message is appropriately entangled and then two path modes are removed. The decompression process is exactly the inverse of the compression process and finally the fidelity of the reconstructed message is measured. A whole process can be implemented by linear optics and APDs. In the experiment, we observed the fidelity better than the maximally achievable fidelity by classical compression (compression without entangling operations). This is a clear demonstration of quantum source coding theorem.
<Reference>
- "Experimental demonstration of quantum source coding," Y. Mitsumori, J. A. Vaccaro, S. M. Barnett, E. Andersson, A. Hasegawa, M. Takeoka, and M. Sasaki, Phys. Rev. Lett., 91(21), 217902 (2003).
(3) Quantum channel coding
We have also demonstrated the basic principle of quantum channel coding, so-called the super-additive quantum coding gain. The amount of information transmissible through a channel is determined by the noise characteristics of the channel and by the amount of available transmission resources, such as signal power, and bandwidth. Now let us suppose that we can double the transmission resources, for example, by doubling the signal power or by doubling the bandwidth. Then in conventional information theory, the capacity can be increased twice at most, and never more than that. In quantum information theory, however, the capacity can be increased even more than twice, which is impossible in classical information theory. This feature is called the super-additive quantum coding gain. This will be of practical concern in any transmission of signals at the quantum level where signals are conveyed by non-commuting density matrices. (Classical information theory describes the special case of the signals prepared in commuting density matrices.)
To demonstrate the super-additive coding gain, we consider a particular set of the ternary letters {0, 1, 2} conveyed by the symmetric states of a qubit system, 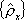 whose elements are
whose elements are ![]() with
with
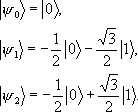
Here {|0>,|1>} is the orthonormal basis set. This letter state set shows the largest amount of the coding gain with the minimum code length, n=2, among the known codes. If  were prepared in commuting density matrices, they could be distinguished perfectly, and log23 [bit] of information (the maximum Shannon entropy of the set {0, 1, 2}) could be faithfully retrieved per letter, meaning that the capacity would be log23[bit/letter]. Distinguishing these states, however, is always associated with finite errors due to the non-commutativity. In fact, the average error probability can never be lower than 1/3 when they are used with equal prior probabilities. The amount of transmissible information therefore reduces to 0.6454 bits of information. We prepare two kinds of ternary letter sets, i.e. the polarization qubit and the location qubit by introducing the two spatial optical paths, and make the code words of length two. According to classical information theory, the total amount of information transmitted with these code words can never be greater than 1.2908 bits. On the other hand, if we apply quantum collective decoding where the polarization and location qubits of a received code word are first entangled appropriately, and then detected, we have confirmed that the amount of 1.312 bits of information is retrieved by our decoder. This clearly shows that transmissible information can increase more than twice when the spatial bandwidth of photon is doubled.
were prepared in commuting density matrices, they could be distinguished perfectly, and log23 [bit] of information (the maximum Shannon entropy of the set {0, 1, 2}) could be faithfully retrieved per letter, meaning that the capacity would be log23[bit/letter]. Distinguishing these states, however, is always associated with finite errors due to the non-commutativity. In fact, the average error probability can never be lower than 1/3 when they are used with equal prior probabilities. The amount of transmissible information therefore reduces to 0.6454 bits of information. We prepare two kinds of ternary letter sets, i.e. the polarization qubit and the location qubit by introducing the two spatial optical paths, and make the code words of length two. According to classical information theory, the total amount of information transmitted with these code words can never be greater than 1.2908 bits. On the other hand, if we apply quantum collective decoding where the polarization and location qubits of a received code word are first entangled appropriately, and then detected, we have confirmed that the amount of 1.312 bits of information is retrieved by our decoder. This clearly shows that transmissible information can increase more than twice when the spatial bandwidth of photon is doubled.
<References>
- Exceeding classical capacity limit in quantum optical channel," M. Fujiwara, M. Takeoka, J. Mizuno and M. Sasaki, Phys. Rev. Lett., 90(16), 167906 (2003).[PDF 206KB]
- "Implementation of generalized quantum measurements: Superadditive quantum coding, accessible information, and classical capacity limit," M. Takeoka, M. Fujiwara, J. Mizuno, M. Sasaki, Phys. Rev. A, 69(5) 052329/1-14 (2004).

