中央集権型の集団では、一人のリーダーが集団の個々のメンバーに命令することによって秩序を構築します。一方、群れ飛ぶ鳥や群泳する小魚、あるいは混雑した駅構内での人間などは、それぞれの個体が隣接する個体との距離や速度などによって定まる局所的なルールに従うだけですが、これらの積み重なりによって高度な秩序が生み出されています。このような鳥や魚などのように自分で動くことができる個体 (自己駆動粒子)が動的に作り出す集団運動は、そのボトム・アップ的に生じる性質が注目され、理論的な研究がなされてきました。しかしながら、対象となる実験系が主に生物の集団であり、局所ルールに不明瞭な部分がぬぐえないため、理論的な研究と実験的な研究が直接比較されることが難しい状態にあり、実験・理論の相補的発展が妨げられていました。
独立行政法人 情報通信研究機構(以下「NICT」、理事長:宮原 秀夫)は、将来の情報通信技術への応用を探る基礎研究として、生体分子の物性や機能の研究を行っており、その一環として、生体分子の自己組織化メカニズムを解明する萌芽的な研究を行っています。
今回、NICT(大岩 和弘)、愛知教育大学教育学部(住野 豊)、東京大学大学院理学系研究科(永井 健)、京都大学大学院理学研究科(吉川 研一)、CEA-Saclay, France(Hugues Chaté)等の研究グループは、生体分子の自己組織化現象を新たに見いだし、その数理モデルの構築に成功しました。この現象は、細胞の運動に関わるタンパク質モータであるダイニンが、マイクロメートルの長さのタンパク質フィラメントである微小管 を基板平面上で運動させる際に、微小管同士の衝突の繰り返しによって、動的な渦の配列構造が自発的に生成されるものです。この渦の配列構造は、構成要素であるタンパク質のサイズより1000 倍から100 万倍も大きい規則構造と言えます。微小管の持つ運動の記憶とも呼ぶべき一時的な運動方向の偏りと、衝突の際の局所的相互作用を規定する単純なルールを仮定した数理モデルは、実験の結果を半定量的に再現することに成功しました。本研究は、高等生物(魚・家畜)を含む自己駆動粒子の集団運動様相の理解及びその制御へとつながる知見となるほか、ボトムアップ的に構造形成を行う必要がある分子情報通信デバイス構築技術の実現に向けた重要な知見となると考えられます。
なお、この成果は、国際的科学誌Nature 2012 年3月22日号(電子版:米国3月21日(水) Eastern Time 14:00)に掲載されます。
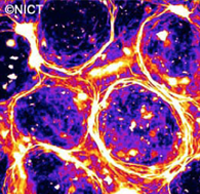
今回、タンパク質モータとその運動の軌道となるタンパク質フィラメントの相互作用によって生じる自己組織化を見いだしました。真核生物の繊毛や鞭毛の運動を引き起こすタンパク質モータであるダイニンとこの軌道となる微小管を使って、ダイニンを吸着させたガラス表面を滑走運動する実験系を作成し、微小管集団の運動を蛍光顕微鏡で観察しました。微小管は互いに衝突しながら、やがて運動の向きをそろえはじめ、何本もの太い流れを作り出しました。さらに、運動開始から10 分ほどで突如として大きな渦パターンが出現し、これらが整列することも確認されました。
個々の微小管の運動及び衝突時点での微小管の挙動を解析することで、この現象の背景にある物理的要素を簡潔な数理モデルにしました。この数理モデルは、集団運動の生成を記述するための最も単純なモデルの一つであるVicsek モデルを拡張したものとなっています。実験的に得られた微小管の相互作用とその運動特性をそのまま数理モデルに当てはめることで、実験で見いだされた集団運動を正確に再現することができました。
この数理モデルに基づき実験結果を解釈すると、本研究で見いだされた巨大な渦の配列構造は、短時間の記憶を持つ自走粒子が十分に多数集まることで、個々の粒子の運動様相の記憶が集団として増強され生じたものと言えます。このように、集団化によって個々の短時間の記憶が集積する様子を示す単純かつ再現のよい実験系の発見は、自己駆動粒子一般の集団運動を理解する上で重要なステップとなると考えられます。
直接的な応用としては、ナノメートルサイズの粒子が1000倍から100万倍の大きさの構造を自律的に創る仕組みの数理モデル化によって、材料分野における所望の構造を自律的に形成する場合の設計指針に応用できると考えられます。また、Vicsek モデルに近い数理モデルを用いた人間の集団行動の研究として、火事などの災害時の緊急避難の解析が行われている現状をかんがみると、今回発見した微小管の運動のような短期的な記憶を伴う自走粒子の運動を実験的及び理論的に研究することは、避難時や渋滞時の人間の集団運動の解析や集団秩序の制御、あるいは畜産や漁業での家畜の群れや魚の群れの効率的な制御を行うために有用な知見を与えることにつながると考えられます。
なお、この研究成果は、Nature 2012年3月22日号に掲載されます。
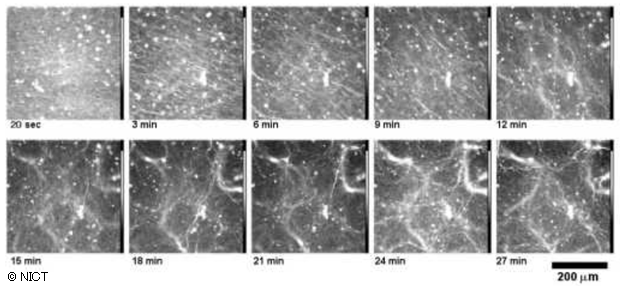
運動開始時からの時間経過を示す。3分、6分ほどで微小管の束が出来上がり、何本もの水平方向に流れが見える。その流れの向きは水平方向から垂直方向に回転を始め(9分~12分)、突然、渦状のパターンが形成される(12分~15分)。
個々の微小管はこの図では見えていない。
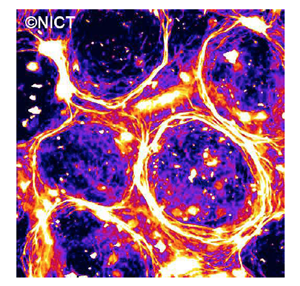
それぞれの渦の直径は400μm(マイクロメートル)ほどである。この渦は時計回りと反時計回りに渦の中を動く微小管から形成されている動的構造である。
補足資料
タンパク質モータは、大きさが10~50nm(ナノメートル)ほどのタンパク質で、生命の運動に関わるタンパク質です。ATP(アデノシン三リン酸)を加水分解して、そこから得られるエネルギーを使って、タンパク質フィラメントの上を滑るように運動することができます。代表的なタンパク質モータには、筋肉の収縮を引き起こすミオシン、細胞の中の物質輸送を担うキネシン、鞭毛や繊毛の波打ち運動を作る出すダイニンがあります。それぞれのタンパク質モータは、タンパク質フィラメントと相互作用して運動することができます。ミオシンはアクチンと、キネシンとダイニンは微小管と相互作用して動きます。微小管は、直径25nm(ナノメートル)ほどで長さが10μm(マイクロメートル)に及ぶ細長い中空のフィラメントです。生物から抽出して精製したタンパク質モータをガラス基板の上に吸着させ、この上にタンパク質フィラメントを加えて、エネルギー源であるATP を添加します。すると、タンパク質フィラメントは、まるで生き物のようにガラス基板上をはいまわります。このような実験系をin vitro 運動アッセイと呼びます(図3)。
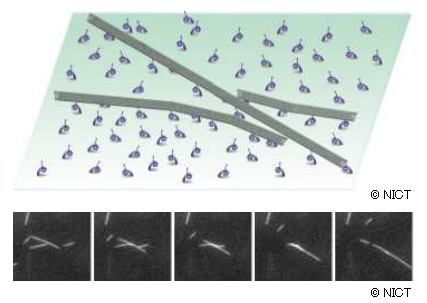
本研究では、ダイニンと微小管を使ってこのin vitro運動アッセイを行いました。ガラス表面に吸着させたダイニンの上を長さ10μm(マイクロメートル)ほどの微小管が運動します。 このとき、微小管の運動方向はランダムであるために、時々、ほかの微小管と衝突することがあります。衝突の際に微小管同士が寄り添うように振る舞います。たくさんの微小管が衝突を繰り返すうちに、運動する微小管が集まってきて、双方向に運動する微小管からできた大きな流れが出現します。10分ほど経つと、この流れの中にたくさんの渦が出現します。この渦の直径は平均で400μm(マイクロメートル)ほどで、ガラス基板表面(10mm×20mm)を覆い尽くすほどたくさんの渦が一面に出現します(図4)。
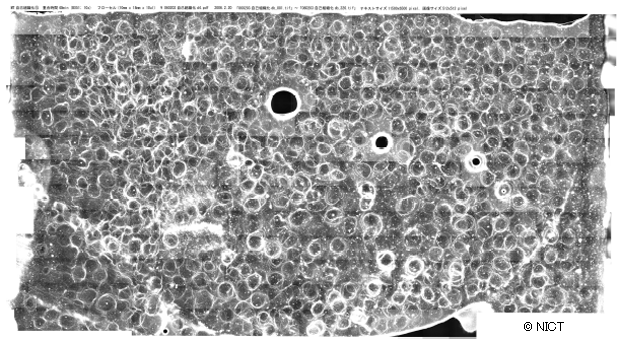
それぞれの渦の直径は400μm(マイクロメートル)ほどの大きさで、隣接する渦は相互作用している。 黒く見えるのは、実験槽に入りこんでしまった空気の泡で、この周りには、渦は形成されていないことが分かる。
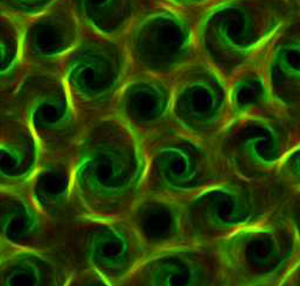
この数理モデルでは、短時間の記憶(運動方向の偏り)を持つ能動的な粒子が多数存在する系を理論的に構築しました。この粒子を多数導入し、計算機シミュレーションを行ったところ、粒子が十分に多数集まることで、運動様相の記憶が集団として増強され、空間サイズが1000倍も異なる秩序構造、渦列構造が現れることを見いだしました(図5)。これはin vitro運動アッセイで得られた自己組織的渦形成と同じものです。
個々の粒子の運動について見てみると、運動する粒子が持つ記憶(運動方向の偏り)という特性は,運動のきが同じ方向にそろい寄り添う、あるいは逆方向にそろいすれ違うという相互作用を通じて伝えあっています。寄り添って運動する場合に比べて、すれ違いによる相互作用は、粒子にとって時間的には一瞬の出来事ですので、少数の粒子の相互作用においては大きな効果はありません。しかしながら、多数の粒子が存在する状態においては、すれ違いによる相互作用が記憶情報の交換の点で重要となります。多数の粒子が衝突してすれ違いを続けることで、集団全体としてある種の記憶の共有がなされることとなり、粒子サイズに比べてはるかに巨大な秩序構造が生成するのです。
この自走する粒子の集団運動のモデル化は、避難時や渋滞時の人の集団運動の解析につながるものです。これまでに人の集団運動の研究としては、Vicsekモデルに近い数理モデルを用いたものがあります。例えば、火事などの災害時の緊急避難の解析がこれを用いて行われており、効率な避難方法の提案などにつながっています。また、非常に多くの人間が集まるある種の祭典では、交通渋滞が起こり、圧死などが問題となっている例があり、政府がこの問題解決を数学の専門家に依頼するなど、人間の集団制御に関しては、基礎研究サイドからの成果が期待されているところです。
今回の成果は、自走粒子集団の秩序的な運動であり、この現象を応用すれば人の集団秩序の制御への応用につながると期待されます。また、人間以外にも羊の群れや魚の群れの効率的な制御を行うことで、畜産や漁業などにも有用な知見を与えることになると期待できます。
また、ナノメートルサイズの粒子が動的に1000倍から100万倍のスケールの違う規則構造を作る原理の解明は、分子を用いた情報処理素子などのボトムアップ的構築技術を要する素子開発の開発指針を与えるものと考えられます。
(住野 豊(愛知教育大学教育学部)、 永井 健(東京大学大学院理学系研究科)、 志鷹 祐司(NICT)、 田中 ダン(名古屋大学大学院情報科学研究科)、 吉川 研一(京都大学大学院理学研究科)、 Hugues Chaté (CEA-Saclay, France)、 大岩 和弘(NICT、兵庫県立大学大学院生命理学研究科)
用語解説
氷やミョウバンの結晶成長、シャボン玉の薄膜の形成等、ランダムな状態から秩序のある状態へ、あるいは微視的要素が巨視的構造に自分で勝手に組み上がっていく現象を「自己組織化」と呼ぶ。結晶成長などが平衡系の自己組織化の代表例であるが、魚の群泳など、より動的な構成要素から成る非平衡系の自己組織化もあり、このメカニズムの解明は現代科学の大きな研究テーマになっている。
CEA は、独自の優れた基礎研究実績と多岐にわたる専門知識を駆使し、多くの教育機関及び産業界のパートナーと多数の共同プロジェクトを推進している。現在、CEA の職員数は、研究者・技術者・事務職を合わせて16000人に上り、欧州研究ネットワークにおいて主要的地位を占めている。
生物の運動の原動力となっているタンパク質である。ATP(アデノシン三リン酸)を加水分解したときに得られるエネルギーを使って、タンパク質フィラメント の上を運動することができる。代表的なタンパク質モータは、筋肉の収縮の原動力であるミオシン、細胞内の物質輸送に関わるキネシン、繊毛・鞭毛の運動を作 り出すダイニンがある。
真核生物の鞭毛や繊毛の運動を作り出すタンパク質モータ。大きさ50nm(ナノメートル)ほどのタンパク質であり、ATP(アデノシン三リン酸)の加水分解で得られるエネルギーを使って微小管の上を滑るように運動する。
ダイニンやキネシンの運動の軌道となるタンパク質フィラメント。球状タンパク質であるチューブリンが重合してできたフィラメントで、直径25nm(ナノメートル)の中空の筒である。重合の程度で微小管の長さは変えることができる。この実験では10〜15μm(マイクロメートル)ほどの長さの微小管を用 いている。
外部あるいは化学反応によりエネルギーの注入を受け動く粒子の総称。具体的には周りから揺すられた粒子や、昆虫、動物や人間、自動車など様々な"動くもの"を表す。
自己駆動粒子が集合することで生じる協同的な運動様相のこと。外部からの指示、あるいは群れを操るリーダーが不在にもかかわらず、全体として秩序ある運動が生じる。具体例として、魚の群れ運動や車の渋滞現象が挙げられる。
Tamas Vicsek により提唱された自己駆動粒子の数理モデル。粒子の運動速度を一定に保つ、相互作用はすぐ近くの粒子とのみ行う等、大胆な単純化を行ったモデルである。このような単純化にもかかわらず、実験で見られる様々な集団運動を記述することができる上、異なる"動くもの"の集団運動の背後に潜む数理構造に近づく手がかりともなっている。
本件に関する 問い合わせ先
大岩 和弘
Tel: 078-969-2110
Fax: 078-969-2114
携帯: 090-5095-7174
E-mail: 


取材依頼及び広報 問い合わせ先
廣田 幸子
Tel: 042-327-6923
Fax: 042-327-7587
E-mail: