はじめに
現代社会を支える公開鍵暗号技術として、主にRSA暗号と楕円曲線暗号が使われています。しかし、これら2種類の暗号は量子コンピュータを使うと簡単に解読されてしまうことが20年程前に数学的に証明されています。そのため、量子コンピュータを用いても(そしてもちろん普通のコンピュータでも)簡単に解読することのできない暗号方式を開発し、社会で運用していくための研究が進められています。このような、量子コンピュータでも通常のコンピュータでも解くことが難しい暗号は耐量子計算機暗号と呼ばれ、その候補としてさまざまなものが提案されています。
耐量子計算機暗号として新たに提案された暗号方式には、解読が難しいだけではなく、RSA暗号や楕円曲線暗号にはない様々な特徴、例えばクラウド・コンピューティングにおいて計算内容の機密保持に使える、大きな組織内での情報管理に向いている等の特徴を持っています。これらの暗号は、それぞれの特徴を活かして耐量子計算機暗号のデファクトスタンダードを狙っているため、さながら戦国時代のようになっています(図1)。
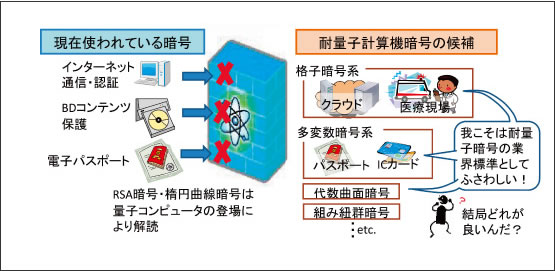
図1 耐量子計算機暗号の業界標準に向けて
解読実験 ―暗号実用化のための基準作り―
提案された暗号方式の中で一番良いものはどれか、ということを誰もが納得する形で比較するため、統一された基準を作る必要があります。例えば、同じ暗号方式であれば、鍵長が長い(パラメータが大きい)方がより安全であることが直感的にわかりますが、異なる暗号方式の場合には鍵長による単純比較は行えません。
しかし例えば、「世界一高速な解読プログラムを用いて、スーパーコンピュータ京でも解読に1年以上かかる」という安全性を同レベルに設定した上で、実際に利用する場合の暗号化速度の比較を行えば、異なる暗号方式同士でも優劣をつけることができます。実際には、解読プログラムもスーパーコンピュータも日々進化し続けているため、解読実験の結果から、スーパーコンピュータでの解読に1年以上かかるための数年後のパラメータはどれくらいで、このデータ量の下限は何バイトになっているという予測を行うことで、各暗号方式の安全性の比較評価を行うことができます(図2、3)。
耐量子計算機暗号の候補となっているいくつかの暗号方式に対して、このような評価を行うことにより、実用化の場面ごとに最適な方式を選ぶための基準作りを行うことができます。このたびセキュリティ基盤研究室では、候補のひとつである格子暗号の解読に現れる「最短ベクトル問題」の難しさの評価を行いましたので、以下に報告をします。
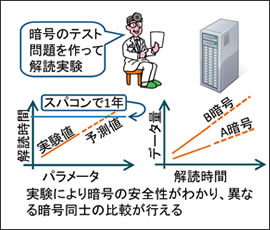
図2 解読実験による暗号の比較
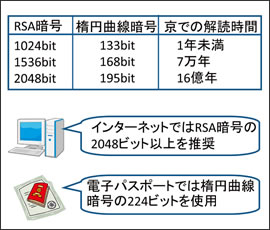
図3 解読実験による暗号の比較と実社会での応用
格子暗号
格子暗号の概念図を図4に示します。格子とは、図の(A)、(B)のように空間内に規則的に並んだ点の集合(図は2次元空間の例)であり、コンピュータの内部ではベクトルの集合(図中の黒矢印の組)として表現されます。このベクトルを適当に整数倍して足すことで、すべての格子点を網羅することができます。
格子暗号を用いた通信は、メッセージの送信者が受信者に対して通信処理の要求を出した後、①準備、②暗号文の生成・送信、③メッセージの復元の3ステップで行われます。
① 要求を受けた受信者はまず、図4(B)のような直交に近いベクトルの集合(黒)と、対応する少し斜めになっている格子(青)を生成します。このベクトルの集合(黒)を使うと暗号文を復号できるため、これは秘密情報としておきます。次に、斜めになっている格子の情報をメッセージ送信者に送る必要がありますが、秘密情報のベクトルをそのまま送ってしまうと途中の盗聴者も暗号文を復元できてしまうため、暗号の意味がありません。そこで、同じ格子点を網羅するようなベクトルの集合で、暗号文の復元には使えないように変形したものを送ります。図4(B)の赤い2本のベクトルがそれで、ベクトル同士が互いに平行に近いときには、暗号文の復元には使えないことが知られています。
② メッセージ送信者はベクトルの集合を受け取ったのち、それらを適当に整数倍して足して座標を計算します。この座標は、受信者が生成した格子点のひとつになっています。この座標をさらに、送りたいメッセージの分だけずらして、受信者に送ります(図4(C))。このとき、ずれとメッセージの対応はあらかじめ決められているものとします。
③ 座標のデータを受け取った受信者は、送られてきた座標情報の一番近くにある格子点を計算で求め、ずれを計算し、そこからメッセージを復元します(図4(D))。
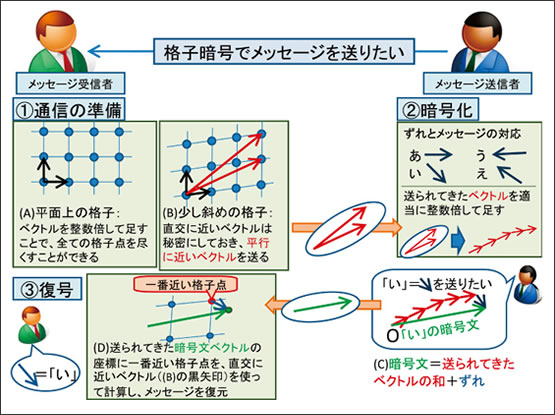
図4 格子暗号のイメージ
格子暗号の安全性
送信者が送った点の座標から、メッセージに対応するずれを計算するためには、座標に一番近い格子点を求める必要があります。この計算は、格子を表現するベクトル集合が図4(B)の黒いベクトル集合のように互いにほぼ直交しているときには、高速に行えることが知られています。逆に、赤いベクトル集合のようにほぼ平行であるときには、計算は非常に時間がかかると予想されているため、盗聴者がほぼ平行なベクトル集合と暗号文の座標を手に入れても、その情報だけから暗号を解読することは難しく、格子暗号は安全であると考えられています。
反対に、もしも盗聴者がほぼ平行なベクトル集合からほぼ直交なベクトル集合を復元することができれば、どのような暗号文も解読できてしまうため、この復元が行えない程度のパラメータを取る必要があります。現在、ベクトルの本数が800本(800次元)程度であれば復元可能であることが実験により確認されており、今後もこの本数は上がり続けていくと考えられます。
最先端アルゴリズムによる解読実験
我々は暗号の解読実験を行うため、ベクトル集合の復元を行う最新のアルゴリズムを改良しました。ほぼ平行なベクトル集合からもとの集合を復元する計算は、一気に全てのベクトルを扱おうとすると非常に大変なものとなります。そのため最新のアルゴリズムでは、図5のようにベクトル集合の中から100本程度取り出してそれらをほぼ直交なベクトル集合に直し、もとの集合に戻してまた別の100本を処理する、という操作を繰り返すことで全体を少しずつ直交に近づける計算を行っています。
一般に、ベクトル集合が平行に近いときには、ベクトルは長く(図5(A))、直交に近いときには短い(図5(C))という特徴があります。そのため、与えられたベクトル集合を変形してなるべく短いベクトルを求める問題が暗号の安全性評価に深く関わっています。この問題は最短ベクトル問題と呼ばれ、格子暗号解読コンテストである格子最短ベクトル問題チャレンジ(TU Darmstadt lattice challenge)* では世界中の研究者がこの問題を解くためにしのぎを削っています。既存の研究では、取り出すベクトルの本数が固定値であったため計算中に無駄な箇所があったのですが、我々は取り出す本数の最適値を自動的に計算する手法を確立し、アルゴリズムを改良しました。コンテストにおいて825次元の問題を解き、新たな世界記録を樹立することができました。
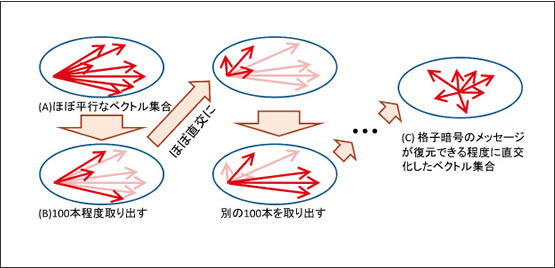
図5 ほぼ平行なベクトル集合を少しずつ直交化していくアルゴリズム
将来の展望
現在、格子暗号の安全性評価に使われているアルゴリズムはメモリの使用が極端に少ないものが主流です。一方、アルゴリズム理論では「時間-空間計算量トレードオフ」と呼ばれるメモリ使用量を増やして計算を高速化する手法(図6)があるため、それを用いて高速化したアルゴリズムでの再評価を行いたいと考えています。また、ベクトルの集合を直交化させるアルゴリズムは、格子暗号以外の評価にも応用できることが知られているため、それらの解読実験も行いたいと考えています。
図6 時間-空間計算量のトレードオフ
 |
青野 良範(あおの よしのり) ネットワークセキュリティ研究所 セキュリティ基盤研究室 研究員 大学院修了後、2011年、NICTに入所。公開鍵暗号の安全性評価に関する研究に従事。 博士(理学) |
![]() 1303号_3-5p(印刷用、1.13MB、A4 3ページ)
1303号_3-5p(印刷用、1.13MB、A4 3ページ)