Quantum control of continuous variable states
This study group is investigating the generation and control of continuous variable entangled state in quadrature amplitude of light. Developing new measurement and standard technologies that make active use of quantum entanglement is also an important mission. Entangled states can be powerful probes for estimating the parameters of quantum channels, measuring nanostructures, and monitoring the electronic states of matters, which otherwise could not be observed with conventional light probes. These will be the basic technologies for frequency standards and electromagnetic sensing of the next generation.
Researchers: J. Neergaard-Nielsen, M. Takeuchi, K. Hayasaka, M. Takeoka, and M. Sasaki
Continuous variable states as qubits (YouTube video)
In a 2010 paper [Phys. Rev. Lett. 105, 053602], we demonstrated how it is possible to generate arbitrary superpositions of two different continuous-variable states, squeezed vacuum and squeezed photon. We use a special ambiguous photon subtraction technique that leaves the output in such a superposition state with predetermined weight and phase.
We generated states with a range of different parameters and did full homodyne tomography of them all. Therefore we can present them as Wigner functions, which are a kind of probability distribution in the continuous phase space of amplitude and phase of the light field. On the contrary, since the states are superpositions of two orthogonal states, we can also represent them as qubits, the basic unit of traditional quantum information theory. The graphical representation of such a qubit is a sphere (the Bloch or Poincare sphere) where squeezed vacuum is located at the north pole and squeezed photon at the south pole.
Continuous variable states as qubits (interactive viewer by Java applet)
In addition, another interactive applet will let you spin and move through this Bloch sphere, where all of our measured states are inserted at their corresponding locations in the qubit space, each of them represented by the Wigner functions. That means you are actually moving through a hybrid continuous variable/qubit space!
Please note that the applet requires Java capability depending on your browser and there may exist some risks due to remote program excution, therefore the page may be closed without any notice.This applet was built with Processing. The source code is also available here.
(1) Entanglement-assisted coding with a two-mode squeezed vacuum
The main subject of our group is to study how to realize the thorough quantum controls of the quadrature amplitude and phase of the light field. The quadrature amplitude and phase of the light field is representative examples of quantum continuous variables (CVs). CV quantum information and communications technology (CV QICT) is an important avenue in QICT as well as discrete variable (DV) approach, such as photon qubit systems. In particular, CV systems are the essential platform of optical communications.
Advanced technology of optical communications adopts the thorough control of wave nature of light. Signals are encoded into multi-array coherent states, by modulating the quadrature amplitude and phase of the light field. A coherent state is only the state, which can propagate in a pure state intact even through a lossy channel. No other states have this property. The coherent states are thus the best signal carrier. The signals are decoded by dyne-type detection, such as homodyne or heterodyne detection, which can observe directly the quadrature amplitude and phase. The performance of this level of technology, the so called coherent communication, is determined by the quantum noise of CVs.
In the quantum domain, one can control the quantum noise by squeezing operation. Squeezed states play an essential role. In particular, a CV entangled state can be generated simply by combining two squeezed states via a beam splitter. Squeezed states and coherent states belong to a family of Gaussian states. Squeezing operation, linear optics and dyne-type detection constitute a class of Gaussian operations. Gaussian operations are readily available in the laboratory and serve as a complete framework for many quantum protocols, including CV quantum cryptography, quantum teleportation, and quantum sensing.
Mathematically Gaussian operations form a closed group, called Clifford semi-group, and Gaussian states are mapped only into Gaussian states. Their dynamics can be simulated classically by tracing the changes of the small set of parameters, the means and variances of Gaussian states. In other words, Gaussian operations are not sufficient to realize fully quantum-enhanced tasks.
In fact, it was theoretically proven that Gaussian operations can never distill the entanglement from Gaussian state inputs [Eisert, Scheel, & Plenio, PRL 89, 137903 (2002)], and also that quantum speed-up of CV processing is impossible only by Gaussian operations [Bartlett, et al., PRL 88, 097904 (2002)]. They are known as the no-go theorems of Gaussian operations. The above important tasks essentially require a new technology of non-Gaussian operations, which are highly non-linear processes with very low loss, which is not an easy task at all.
A currently feasible scheme is photon subtraction from a squeezed state. This conditional process allows one to generate photon number states, Schroedinger cat states, and so on. It can be implemented in the following way (Fig. 1).
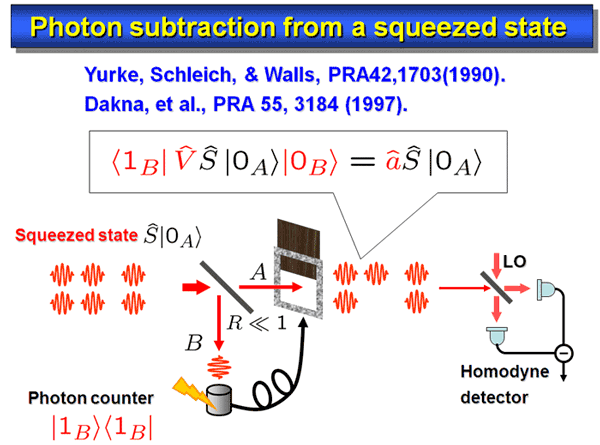
A small fraction of a squeezed beam is tapped at a beam splitter with a small reflectance, and is guided into a photon counter. Only when we have a photon detection right here, we gate the main beam, and observe the conditional state. As the reflectance is set small, this realizes the annihilation of photon from the squeezed state.
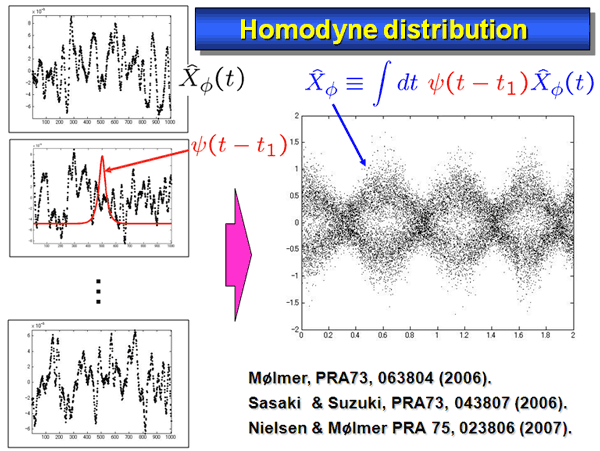
For characterizing the output state, we construct the Wigner functions. This is a method to represent a quantum state by a phase space distribution in terms of the quadrature amplitude and phases. This is a quasi-probability distribution, can visualize various features of quantum states, and is allowed to take negative values. And more importantly, it is known that states with negative Wigner functions can never be described by classical theory. The Wigner function can be obtained by the homodyne tomography. Namely, we measure homodyne distributions for various phases by sweeping the local oscillator phase (Fig. 2).
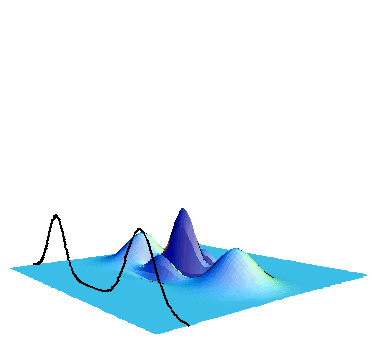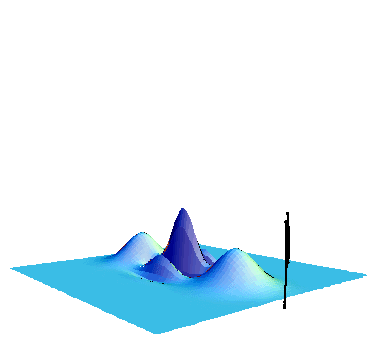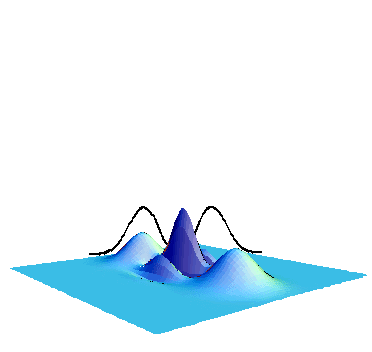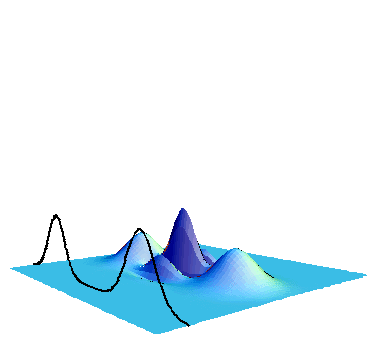
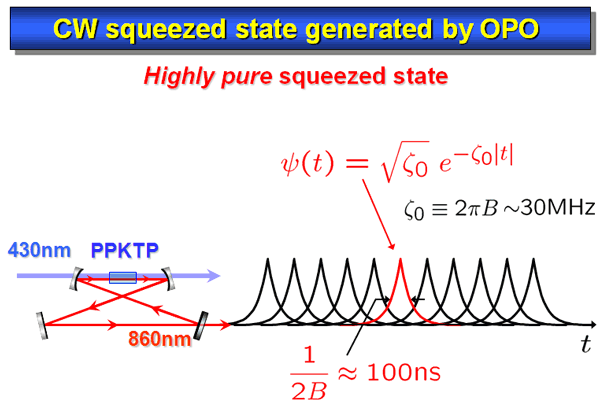
In our experiment, we use a cw squeezed state is generated by an optical parametric oscillator with PPKTP crystal. Intuitively this kind of CW beam is a continuous sequence of squeezed wave packets, whose shape is an exponential function in a typical time scale of 100ns, where ζ0 is the angular-frequency bandwidth of about 30MHz (Fig. 3).
Photon detection at a Si APD, say at a time t_1 specifies a particular wave packet around the t1 in the main signal beam, where a Schroedinger cat state is generated (Fig. 4).
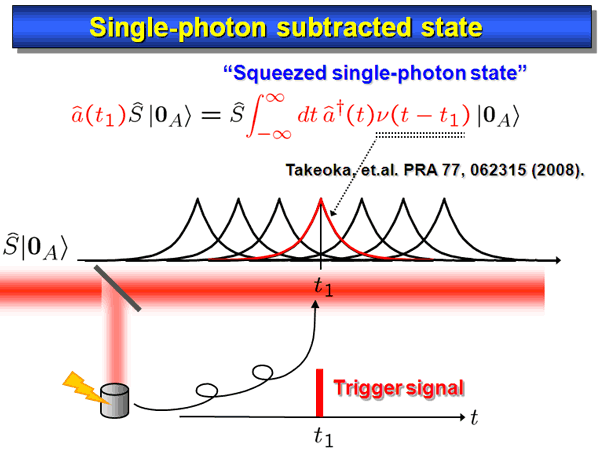
So for every trigger signal, the homodyne current is sampled around the trigger signal time. The continuous homodyne current is multiplied by this mode function, and is then time-integrated to obtain a quadrature value. In Fig. 5, an example of quadrature distribution thus obtained is shown.
In Fig. 6 previous results of the single-photon subtraction are shown.
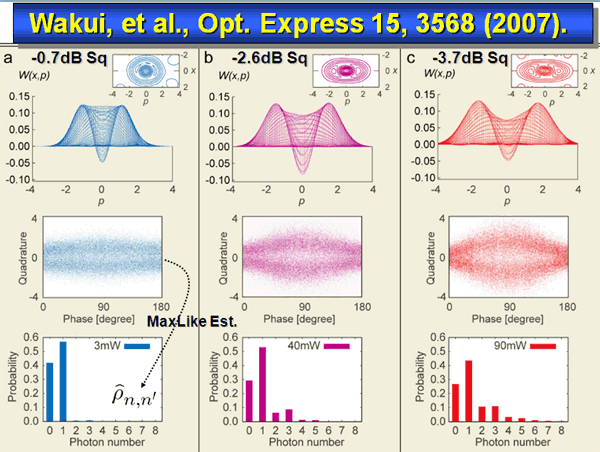
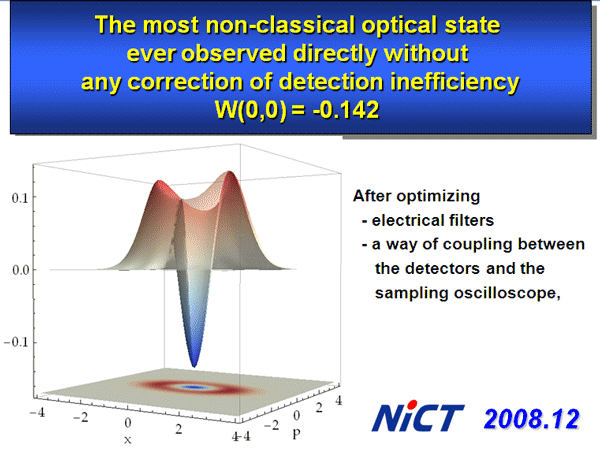
From left to right, we increase the squeezing level. Then the state changes from the single-photon state to odd-parity Schroedinger cats. We have recently improved the non-classicality, namely could have observed much deeper Wigner functions, as shown in Fig. 7.
In the two photon subtraction, we can generate an even-parity cat states. Suppose that there are two photon clicks at t1 and t2. Since the time resolution of Si APD is much shorter than the coherence time of the squeezed state in our case, we can realize the time-separated two photon subtraction within the coherence time. So there are two overlapping temporal packets inside the main “CW” beam. (See Fig. 8.)
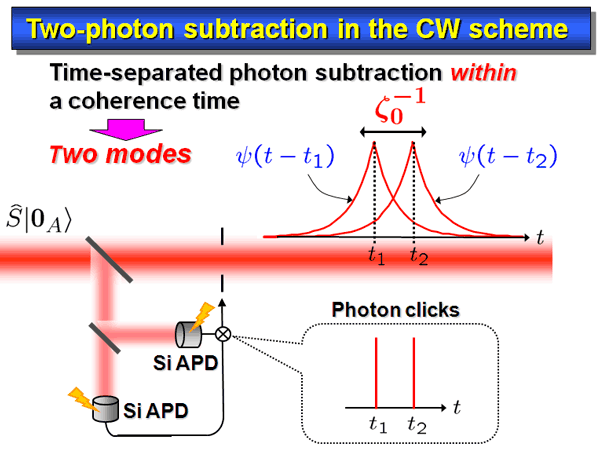
Thus the state is essentially of two modes. We need two appropriate ortho-normal modes. The most natural mode function pair consists of the symmetric mode Ψ+(t) that extracts the cumulative features due to the overlap of the packets, and the asymmetric mode Ψ-(t) that extracts the differential features of these localized packets as shown in Fig. 9.

For relatively small time separation, this symmetric mode contains most of photons, while the asymmetric mode has less photons.
In Fig. 10, the experimental results observed in the symmetric mode are shown.
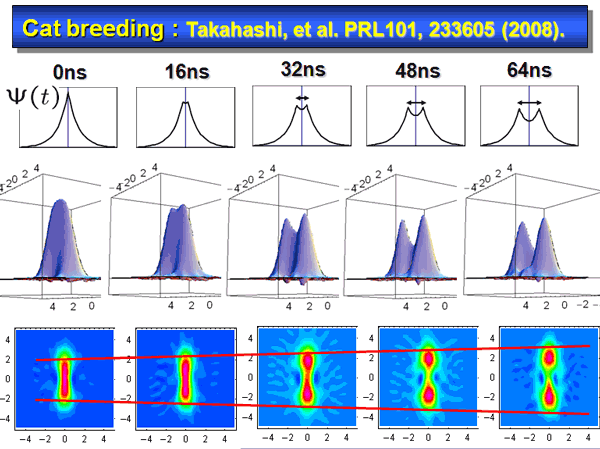
From left to right we increase the time separation. The amplitude of the generated state gradually increases. This kind of amplitude enhancement can be regarded as the breeding of the cat state simply by controlling the time separation.
Fig. 11 shows the average photon numbers in the two modes as a function of the time separation.
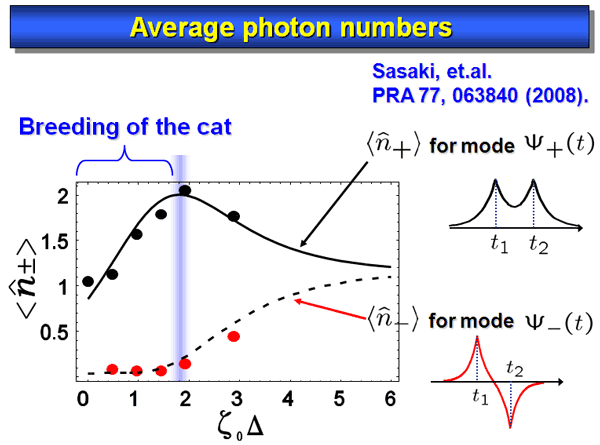
The upper plots are for the symmetric mode, and its rapid increase in this time range is another experimental evidence of breeding the cat state. In the asymmetric mode, there are less photons, but it is essential to realize this enhancement.
For more detail, please see
on single-photon subtraction
Wakui, et al, Opt. Express 15, 3568 (2007).
Sasaki & Suzuki, PRA 73, 043807 (2006).
on two-photon subtraction
Takahashi, et.al. PRL 101, 233605 (2008).
Takeoka, et.al. PRA 77, 062315 (2008).
Sasaki, et.al. PRA 77, 063840 (2008).
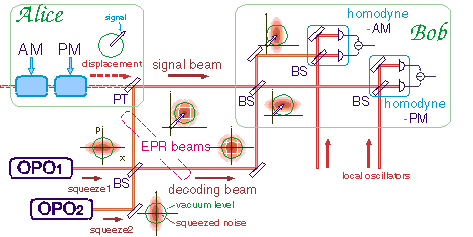
(2) Entanglement-assisted coding with a two-mode squeezed vacuum
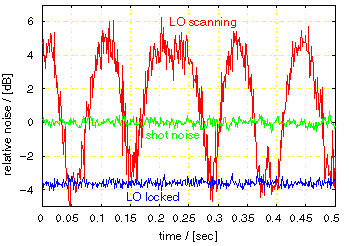
The entangled twin beams described above were generated by the optical parametric oscillator operated above the threshold. Therefore, the quantum correlation was clear in terms of intensity, but the correlation in phase was still insufficient. To realize further advanced protocols for quantum information processing, strong correlation between entangled beams should be formed both in phase and in amplitude. For this purpose, our group is also investigating the generation of multi-mode squeezed states. The single-mode squeezed state is generated by using the non-linear optical effect of KNbO3 (potassium niobate) crystal. Since the non-linear effect of the crystal is so weak, the beam is multiply interacting within the optical parametric oscillator operated below the threshold (Fig. 1). We successfully generated the squeezed vacuum state of -3.6dB in one of our oscillators (Fig. 2).
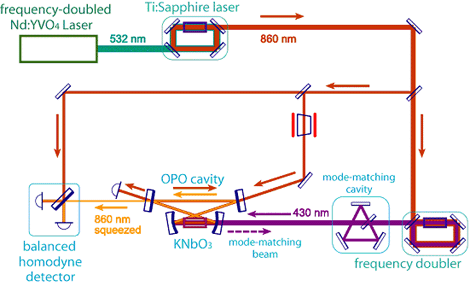
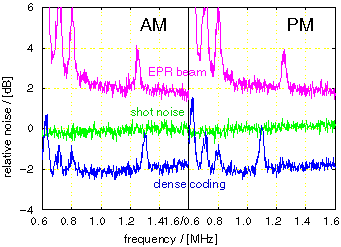
The 2-mode squeezed states can be generated by superimposing two single-mode squeezed states so that their principal axes cross orthogonally. These beams share a notable quantum correlation (EPR correlation), and are utilized in experiments such as quantum teleportation and quantum dense coding. We have carried out the quantum dense coding experiment (Fig. 3) and confirmed (Fig. 4) the noise reduction in the communication channel and the security enhancement against eavesdropping.