Quantum Information Theory
Information technologies are based on 1) the ability to identify objects, 2) efficient expression of information, and 3) correct transmission and processing of the information. These tasks are defined as the problems of signal detection, source coding, and channel coding, respectively and constitute the principal themes of information science. Quantum information theory demonstrates how these problems are generalized to the field of quantum mechanics and identifies the limits of new information transmission and processing methods, by utilizing the quantum effects.
Transmission of classical information and quantum signal detection
One of the fundamental topics of quantum information theory is how to transmit classical alphabets through a quantum limited channel. This subject includes the optimization problem of quantum signal detection, the investigations of the physical models realizing optical detection strategies, and the quantum coding theory which is nothing but quantum information processing with quantum information processing with quantum signal detection.
(a) Quantum signal detection
Quantum siglan detection is mathematically described by a positive-operator valued measure (POVM). The problem here is to find POVMs that optimize the figure of merits, such as minimizing the average error probability of discrimination, maximizing the mutual information for an ensemble of quantum states, and minimizing the Bayes cost of the identification of codes and more complex pattern structures. Physical realization by quantum circuit synthesis of optimal POVMs is also our important concern.
< Selected publications >
"Quantum channels showing superadditivity in capacity," M. Sasaki et al., Phys. Rev. A 58, 159 (1998); quant-ph/9801012.
"Accessible information for real symmetrical quantum sources," M. Sasaki et al., Phys. Rev. A 59, 3325 (1999); quant-ph/9812062.
"Quantum learning and universal quantum matching machine," M. Sasaki and A. Carlini, Phys. Rev. A 66, 022303 (2002);quant-ph/0202173.
"Optimal phase estimation and square root measurement," M. Sasaki, A. Carlini, and A. Chefles, J. Phys. A: Math. Gen. 34, 7017 (2001); quant-ph/0011057.
"Squeezing Quantum Information through a Classical Channel: Measuring the Quantumness" of a Set of Quantum States ," C. A. Fuchs and M. Sasaki, Quant. Inf. Comput. 3(5), 377 (2003); quant-ph/0107024.
(b) Implementation of quantum measurement via linear optics and photon counting
Linear optics and photon counters are powerful and currently (or near future) available devices to realize sophisticated quantum measurement for optical quantum signals. Our goal is to clarify, in principle, which class of quantum measurements can or can not be achieved by using only these devices.
< Selected publication >
"Implementation of projective measurements with linear optics andcontinuous photon counting," M. Takeoka, M. Sasaki, P. van Loock, and N. Luetkenhaus, Phys. Rev. A. 71, 022318 (2005); quant-ph/0410133.
(c) Quantum source coding
This topic aims at the development of efficient methods for expressing information using quantum states. In practice, this topic is related to the compression of quantum data (see Quantum Communication).
(d) Quantum channel coding
This topic consists of the development of methods for correctly transmitting information using quantum states. In practice, this topic is related to error correction (see Quantum Communication).
Control of quantum entanglement and its application
An entangled state is a state where two or more quantum particles are in peculiar quantum correlation, such as in molecular spin singlet. The entangled states were found to be applicable for developing new signal transmission technologies, coding technologies, and signal processing technologies, to which nothing comparable exists in conventional information technologies. Studies have started on information technologies using such new information resources that have no equivalence in classic physics. We are especially studying the generation and control of continuous variable entangled state in quadrature amplitude of light. This is potentially applicable to high-performance quantum teleportation, entanglement assisted communication, and quantum metrology for practical bosonic channels where mesoscopic Gaussian states are the man signal carriers.
< Selected publications >
"Quantum channel of continuous variable teleportation and nonclassicality of quantum ," M. Takeoka, M. Ban, and M. Sasaki, J. Opt. B 4, 114 (2002); quant-ph/0110031.
"Continuous variable teleportation as a generalized thermalizing quantum channel," M. Ban, M. Sasaki, and M. Takeoka, J. Phys. A: Math. Gen. 35, L401 (2002); quant-ph/0202172.
"Optimal parameter estimation of depolarizing channel," M. Sasaki, M. Ban, and S. M. Barnett, Phys. Rev. A 66, 022303 (2002); quant-ph/0203113.
"Unambiguous quantum state filtering," M. Takeoka, M. Ban, and M. Sasaki, Phys. Rev. A. 68, 012307 (2003); quant-ph/0304032.
Generation and control of non-Gaussian states
The main signal carriers in the optical communications are Guassian states, typically the coherent states, which exhibit the optimal transmission proparties through a lossy bosonic channel. Recent theoretical studies show the performance limits attained by Gaussian operations (linear optics, the squeezers, homodyne detections, and classical feedforward) on the Gaussian states. For example, quantum speedup of signal processing is impossible. The distillation of Gaussian entanglement is impossible either only by Gaussian local operations and classical communications (GLOCC).
In order to enjoy the potential benefit of quantum information processing one must go beyond the Gaussian operations. The non-Gaussian operations require the third or higher order Hamiltonians with respect to the optical fields. If one of such nonlinear processes would be applicable, then one can construct, in principle, arbitrary quantum operations by combining it with the Gaussian operations, constituting the universal gate set.
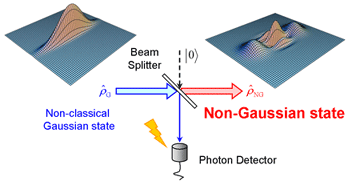
One of the plausible approach to implement such nonlinear gates is to use the nonlinear effect caused by the photon number measurement. The simplest example of such a non-Gaussian operation is shown in Fig. 1. A squeezed beam, which is a non-classical Gaussian state, is tapped off with a beam splitter with a small reflectance. The tapped beam is guided into a photon detector. Photon clicks are used to select the transmitted signal states. The output signal state thus conditioned results in "Schrdinger-cat-like state", which is a non-Gaussian state exhibiting a drastic quantum effect. The theoretical analysis of this scheme including wideband frequency characteristics of squeezed light source and various imperfections is given by
"Multimode theory theory of measurement-induced non-Gaussian operation on wideband squeezed light: Analytical formula," M. Sasaki and S. Suzuki, Phys. Rev. A to appear; quant-ph/0512073.
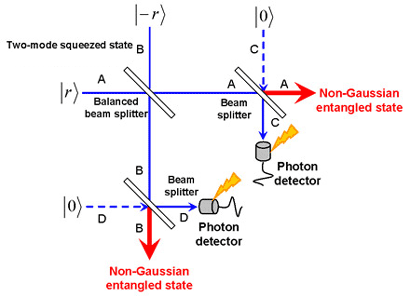
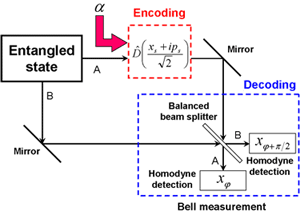
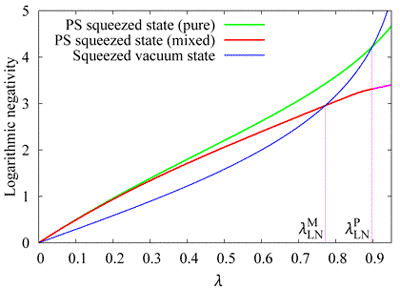
The extension of the above scheme into two beam provides a probabilistic entanglement distillation protocol for the two-mode squeezed state (Fig. 2). The output state is non-Gaussian. For practical photon detectors which fail the precise discrimination of photon numbers, the output state turn out a mixed state. The quantification of entanglement of such a state is highly non-trivial. Our recent results concern the quantification by the mutual information gain in the dense coding scheme as an operational measure (Fig. 3), and by the logarithmic negativity as an monotone measure without any external parameters but an intrinsic entanglement.
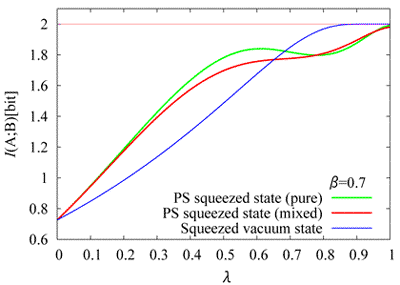
Typical numerical results are shown in Figs. 4 and 5. It was found that whenever the gain is seen in terms of the mutual information of the dense coding (smaller side of ), one can say that the intrinsic entanglement increases as measured by the logarithmic negativity. For further implications and discussions of our results can be seen on the following publications;
"Effective squeezing enhancement via measurement-induced non-Gaussian operation and its application to the dense coding scheme, " A. Kitagawa, M. Takeoka, K. Wakui, and M. Sasaki,
Phys. Rev. A 72, 022334 (2005); quant-ph/0503049.
"Entanglement evaluation of non-Gaussian states generated by photon subtraction from squeezed states," A. Kitagawa, M. Takeoka, M. Sasaki, and A. Chefles, Phys. Rev. A 73, 042310 (2006).