量子コンピュータ時代に向けた新暗号技術を開発
~格子理論に基づき、かつ汎用性に優れた公開鍵暗号を国際標準化に提案~
2018年1月11日
国立研究開発法人情報通信研究機構
ポイント
- 量子コンピュータでも安全な格子理論に基づく公開鍵暗号を開発
- 暗号技術の安全性評価手法を開発、統一的な基準で様々な格子暗号を比較可能に
- 米国NIST主催の量子コンピュータ時代に向けた暗号技術の標準化プロジェクトの候補暗号に
背景
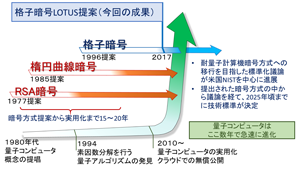
[画像クリックで拡大表示]
今回の成果
今後の展望
補足資料
用語解説
耐量子計算機暗号
現在、社会で使われているRSA暗号や楕円曲線暗号は、ある程度高い性能を持つ量子コンピュータにより、高速に解読されてしまうことが1994年にピーター・ショアによって数学的に証明されている。そのため、このような問題が生じない耐量子計算機暗号への移行を目指した議論が進んでいる。
米国NISTにおける暗号標準化プロジェクト
2016年から、耐量子計算機暗号の標準を決めるための標準化プロセスが開始された。世界中から82件の応募があり、内69件が候補として今後の議論の対象となる。今後3年以上かけ、安全性、実行速度、拡張性などの観点から複数の暗号方式が選ばれる予定である。
参考: 米国NISTの耐量子計算機暗号標準化 ラウンド1候補暗号一覧
量子コンピュータの高性能化・普及
これらの量子コンピュータは、計算問題の種類によっては通常のコンピュータよりもはるかに高速に解を求められることが実証されている。今後も回路規模や扱うことの可能なパラメータ数が大きくなることが予想される。
格子暗号
NICTでは、以前から格子暗号の安全性評価活動を継続しており、今回開発した安全性評価手法は、LOTUSのみではなく、他の格子暗号の評価にも使うことができると期待される。
暗号技術の汎用性
この性質を持たない暗号方式を使う場合、組み合わせ方を間違えるとそこに脆弱性(攻撃者が付け入る余地)が生まれてしまい、システム全体が破たんする危険性があった。システム全体の安全性を保証するためには、暗号一つ一つの安全性を証明した後に、全体の安全性を証明するという二段階の手順を踏む。しかし、複雑なシステムでは専門家が何日もかけて検証しなければならず、また、その複雑さゆえに誤りが発生しやすい等の問題点があった。
暗号を設計する段階で、汎用性という性質を持たせることで、このような危険を避けることができる。汎用性を持った暗号方式同士を組み合わせたシステムは、安全であることが数学的に証明されているため、全体の安全性を証明するステップが省略可能となる。
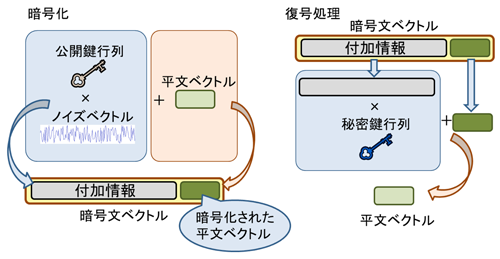
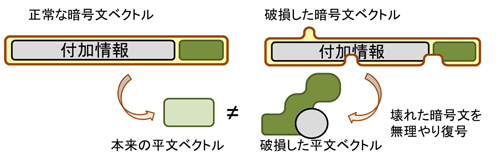
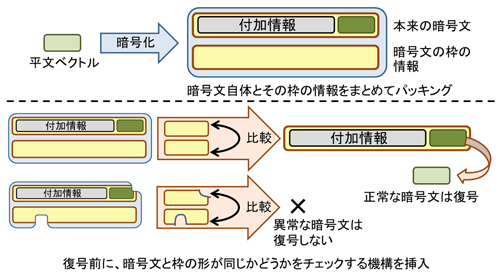
開発したLOTUSでは、ベースとなる格子暗号に対して、復号の際に暗号文の構造をチェックする機構を追加することで、データ破損への耐性を持たせた。このチェック機構により、他の暗号方式と組み合わせ可能な汎用性を持つことが数学的に証明されるため、開発した暗号から様々なシステムを作り、社会の様々な場面で活用することができる。
LWE問題
本件に関する問い合わせ先
サイバーセキュリティ研究所
セキュリティ基盤研究室
青野 良範、レ チュウ フォン
Tel: 042-327-6594
E-mail:


























広報
広報部 報道室
廣田 幸子
Tel: 042-327-6923
Fax: 042-327-7587
E-mail: