通信の基本原理
量子情報理論が予言する新しい情報技術のパラダイムを具現化して行くのは決して生易しい問題ではありません。今後、何十年にもわたって新しい物理原理の開拓や要素技術の開発を進めて行く必要があります。我々の研究室では、量子情報理論の基本原理を、まず現有技術を最大限に活かすこと実証して行くという研究を進めています。
主担当者: 佐々木雅英、武岡正裕
主担当者: 佐々木雅英、武岡正裕
現在の情報技術は、0と1という2つの数字による抽象化の上に成り立っています。実際、パソコンやインターネットの中を駆け巡っている情報の実体は、0と1を運ぶ電気や光の膨大なパルス列です。音声や画像を0と1という抽象的記号で表現することで、効率的なデータの圧縮や雑音下での信頼性の確保が可能になります。いわゆる符号化といわれる操作ですが、それは大きく分けると、データを{0, 1}のビット列で圧縮して表現するための情報源符号化(Source coding)と、そのビット列をできるだけ小さい誤りで伝送するための通信路符号化(Channel coding)の2つに大別されます。この2つの操作を基本要素として情報伝送の基本模型は下図のようなダイヤグラムで整理されます。
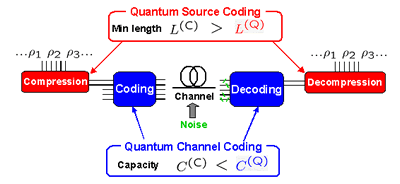
情報源から次々と出てくるアルファベット(ここではρ1, ρ2, ρ3, …)はまず、情報源符号化器によって0, 1の記号系列に変換されます(Compressionの部分)。伝送速度を向上させるためには符号語はできるだけ短いことが望ましいわけです。例えば、出 現頻度が高いアルファベットほど短い符号語で表現することで全体としての平均符号長を節約できます。つまり、出現頻度の偏りは冗長性を意味し、その分、圧 縮した表現が可能なわけです。次に、情報源符号器の出力は、通信路符号器によって通信路の物理的特性に適合した媒体に再度符号化されます(Codingの 部分)。通信路は、光ファイバや電話線であったりコンピュータ内部の半導体メモリであったりするわけですが、こう言った媒体には常に雑音が存在し情報に歪 みや誤りを生じさせます。こういった雑音の効果を予想して、そこで起こりうる誤りを後で訂正できるよう符号語にさらに冗長な0, 1の文字系列を付加するわけです。通信路からの出力系列は、通信路復号器によって誤り訂正を行った後で情報源符号語に復元されます(Decodingの部分)。その後、情報源復号器で情報源符号器の逆変換を行ってアルファベットが復元されます(Decompressionの部分)。
量子情報通信では、上述のアルファベット ρ1, ρ2, ρ3, …は、いまや信号の量子状態を表す密度行列になります。このような領域では、それぞれの符号化操作において量子力学独特の効果が存在し、それを最適に使う ことによって従来の理論限界を超えた操作を実現できます。
- 例えば、信号量子状態ρ1, ρ2, ρ3, …の成分間に非可換性があれば、量子独特の冗長性があり、その分さらなる圧縮が可能になります(Quantum source coding, 新しい平均符号長の下限L(Q) )。
- また受信過程で符号語状態間の量子力学的な干渉効果をうまく引き出すことによって、従来のShannon限界を超える通信路容量を実現できます(Quantum channel coding, 新しい通信路容量の限界 C(Q) )。
このような理論的予言を実験によって検証し、さらに新しい通信技術へ発展させようという研究は、実はまだほとんど手がつけられていないのが現状です。量子暗号や量子テレポーテーションの実験的研究が国内外で急速に進んでいるのとは対照的です。しかし、量子通信路符号化や量子情報源符号化は現在の光 通信技術の自然な延長線上に量子情報技術を発展させて行く上で極めて重要なテーマです。
我々はこれまで量子符号化技術の基礎となる量子信号検出、量子通信路符号化の原理実証、そして量子情報源符号化の原理実証と段階的に取り組んできま した。本格的な量子ゲートを使った符号操作はまだまだ先の話ですが、最近、擬似的単一光子源と線形光学素子を組み合わせた量子回路を用いて、やっと最初の 成果が出始めています。
(1)量子信号検出
レーザ光源の光パワーを減衰させて作る擬似的単一光子源と線形光学素子を組み合わせることで、量子レベルで動作する信号検出回路を開発してきました。これは量子符号化技術の原理実証を進める上で重要な要素技術になります。
<量子信号検出に関する代表的論文>
(2)量子情報源符号化
信号の圧縮とは、信号に含まれる冗長性を取り除く操作です。先にも述べたように,冗長性の典型的な例は文字の出現頻度の偏りです。頻繁偏りがある文章ほ ど、より短い0,1の系列(情報量)で表すこと、つまりデータの圧縮が可能になります。逆に文字の出現頻度に偏りがないデータは、圧縮できないわけです。 しかし量子情報理論と呼ばれる最新の理論によれば、量子力学の世界ではこのような場合でも更なる圧縮が可能になることを予言しています。信号を運ぶ量子状 態には、一般に量子的な重なりが存在しますが、この重なりは、粒子間の量子もつれと呼ばれる相関を適切に制御する事で取り除くことができます。我々は、こ の量子情報源符号化という操作を<世界で初めて実験的に実証しました。
情報の圧縮効率と復元精度は、扱うデータのサイズが大きいほど高くなります。しかし、現在の技術で扱える量子力学的データのサイズは、まだ数ビットにしか 過ぎません。こういった小さいサイズでは、圧縮したデータを完全に元の状態に復元することはできなくなります。したがって、実際上は、どこまで元の状態に 近い状態に復元できるかが問題となります。我々の実証実験では、3ビットの信号を2ビットの信号に圧縮し、再び3ビットの信号へ復元するモデルを使いまし た。実際には一つの光子の直交する偏光面と4本の伝送経路を使って、3ビットの信号を用意します。この信号に対し線形光学素子を使って量子もつれを形成す る適当な変換を行った後に4本の伝送経路のうち2本を捨てることによって、2ビットの信号へと圧縮することができます。圧縮された信号を再び元の3ビット の信号へと復元しその復元精度を測定したところ、量子もつれを使わない従来の圧縮限界よりも高い復元精度が達成されていることが確認されました。
量子的重なりを有する3ビット信号は、図2(b)のように単一光子を半波長板と偏光ビームスプリッタを介して4本の光路へ導波することで用意します。2つ の直交する偏光面と4本の光路で、3ビットの信号を記述する8次元の空間を作るわけです。半波長板の角度をいろいろ変えれば、信号の量子的重なりを調整す ることができます。図2で左側の緑の点線上に量子的重なりを持つ3ビット信号が用意されます。
2ビット信号への圧縮は、4本の光路を2本の光路へ圧縮することで行います。光子の空間的帯域を圧縮するわけです。この圧縮操作は、まず8次元空間 に広がった光子の量子状態に量子もつれを形成するための適切な変換を施し、その後で1ビット分の信号を捨てることで行われます(図2(a))。実際には、 4本の光路のうち2本の光路を2つの半波長板と1個の偏光ビームスプリッタを介して交差させた後、2本の光路のみを残すことで実現します。この2本の光路 と2つの直交する偏光面にわたって広がった4次元上の光子の量子状態が圧縮された2ビット信号を運ぶことになります。
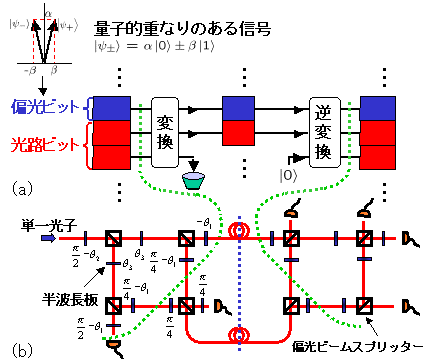
3ビット信号への復元は、圧縮に使った回路とほぼ鏡像対称の回路によって行われ、図1で右側の緑の点線上に3ビット信号が復元されます。これより右側の回 路は、復元された信号の状態が圧縮前の状態にどれだけ近いかという復元精度を測定するための回路です。一方、量子もつれを使わない従来の圧縮は、3ビット の信号に何も手を加えずにただ1ビットを捨てるという操作に対応します(図3)。我々の実験では、この量子もつれを使わない圧縮操作を超える復元精度を実 現することに成功しました。
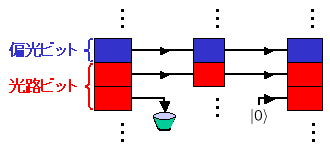
実際の実証実験では、このような操作を単一光子のレベルで正確に行ってやる必要があります。符号化回路は、光を完全に遮断した空間において、そこへ強く減 衰させたレーザーから光子を一つずつ導いて、符号化操作を光子レベルで実行してゆきます。光源には波長632nmのHe-Neレーザーを使い、光子の検出 にはシリコンのアバランシェ(雪崩)増幅検出器を用いています。
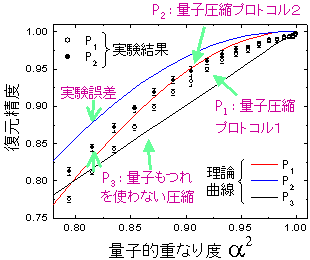
図4は、量子的重なり度合いの異なる信号における圧縮・復元精度測定の実験結果をプロットしています。復元の過程では、単純に圧縮の逆変換を行う方法(プ ロトコル1)と、圧縮過程の結果に依存して逆変換の過程で光子を新たに加える方法(プロトコル2)の2種類の実験を行いました。いずれの方法においても、 理論的に予想される限界の95%程度の精度での実験に成功し、図4から信号の量子的重なり度合いが大きな場合に、量子もつれを使わない圧縮操作に比べて高い復元精度が達成されていることがわかります。
本研究の成果は、改ざんや盗聴に対する絶対安全性を備えた量子暗号技術と組合わせることで、将来、大容量でかつ絶対安全な量子メモリの開発に役立つものと 期待されます。また、微弱な光信号を扱わなければならない深宇宙光通信等で、データを一時的に保存したり、中継する際の新しい技術としても期待されます。
<文献情報>
Y. Mitsumori, J. A. Vaccaro, S. M. Barnett, E. Andersson, A. Hasegawa, M. Takeoka, and M. Sasaki,
"Experimental Demonstration of Quantum Source Coding",
Phys. Rev. Lett. 91(21), 217902 (2003).
Y. Mitsumori, J. A. Vaccaro, S. M. Barnett, E. Andersson, A. Hasegawa, M. Takeoka, and M. Sasaki,
"Experimental Demonstration of Quantum Source Coding",
Phys. Rev. Lett. 91(21), 217902 (2003).
(3)量子通信路符号化
(1)の量子信号検出技術をもとに、超加法的量子符号化利得と呼ばれる量子通信路符号化の基本原理を実証することに成功しました。この原理は、伝送に使う 搬送波の信号パワーや帯域を2倍に増やした時に、伝送できる情報量が2倍以上に増えるという原理です。これは不確定性原理が支配する極限的状況(正確には、非可換性な信号量子状態 ρ1, ρ2, ρ3, …を用いて情報を伝送する状況)で現れる量子力学的効果で、従来の情報理論の範疇ではありえない新しい効果です。
我々はこのような不確定性原理が支配する極限的状況を実現するために、完全に光を遮断した空間に光子を一個一個導いて、符号化を行う光回路を作りました。 符号化は、光子の偏光面を120度の等間隔離れた角度で変調し、0,1,2の3値で行います。このような3値の光子信号には、量子力学的不確定さが伴うた め、光子が運んで来た信号が0,1,2のどれだったかを完全に識別することは、原理的に不可能になります。これを不確定性原理が支配する通信路のモデルと して使います。具体的には、図5に示すような互いに120度離れた単一光子の偏光面の量子状態 |ψ0>,|ψ1>,|ψ2> で表して伝送します。 |ψ0>は、光子の量子状態を表す記号です。
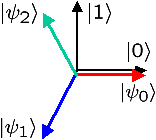
これらの単一光子を使った3元対称偏光信号は、どんなに理想的な検出器を使っても、実は完全に識別することは不可能です。量子力学の不確定性原理のためで す。もし、それぞれの偏光状態が非常に多くの光子からなる場合か、あるいは単一光子でも水平偏光と垂直偏光の2値(|0>,|1> )だけで変調する場合のみ、完全な識別が可能になります。このように単一光子からなる3値信号は、不確定性原理が直接支配する通信路のモデルを提供するわ けです。このような状況で超加法的量子符号化利得という効果が意味を持ってきます。
図6は3値符号化の図式です。もし、3値の偏光状態が多くの光子からなっていて完全な識別が可能であれば、1つの偏光信号あたりlog23(=1.585)ビットの情報量を運ぶことができるのですが、単一光子の場合、不可避な識別誤りが伴うため、送れる情報量は1つの偏光信号あたり最大でも0.645ビットに制限されてしまいます。
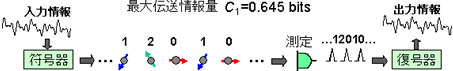
次に、0,1,2を1個の光子ではなく、それぞれ|ψ0>![]() |ψ0>,|ψ1>
|ψ0>,|ψ1>![]() |ψ0>,|ψ1>
|ψ0>,|ψ1>![]() |ψ1>,|ψ2>
|ψ1>,|ψ2>![]() |ψ0>,|ψ1>
|ψ0>,|ψ1>![]() |ψ2>という2個の光子からなる3値の偏光量子状態に載せて運ぶ方法を考えます(図7)。 |ψ0>
|ψ2>という2個の光子からなる3値の偏光量子状態に載せて運ぶ方法を考えます(図7)。 |ψ0>![]() |ψ0>,|ψ1>
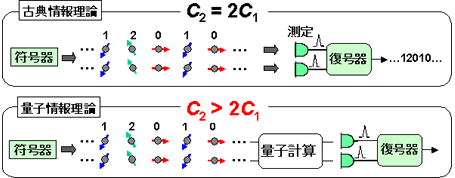
|ψ0>,|ψ1>![]() |ψ0>は、水平に偏光した光子のパルスが2つ並んで飛んでいる状態を表します。このとき、1つの偏光光子対当り伝送される情報量の最大値をC2と書くことにすると、従来の古典情報理論では C2 = 2C1であり、伝送される情報量は最大でも2倍までしか増えません。一方、量子情報理論によると伝送される情報量を2倍以上に増やす、つまり C2 > 2C1と することが可能であると予言されています。この違いをもたらす要因は、信号を取り出す復号過程に量子力学の法則を取り込むか否かにあります。具体的には、 量子状態から信号を取り出す過程で、量子もつれを形成させながら測定を行うことで、古典情報理論の確率法則を超えた復号操作が可能になります。これは測定 を行う前に光の量子状態のままで量子計算を実行することに相当します。0,1,2を運ぶ光子の数をさらに増やして、一般にn個にすると情報量は C2 = nC1とさらに増えてゆきますが、増加の比率は一定値
|ψ0>は、水平に偏光した光子のパルスが2つ並んで飛んでいる状態を表します。このとき、1つの偏光光子対当り伝送される情報量の最大値をC2と書くことにすると、従来の古典情報理論では C2 = 2C1であり、伝送される情報量は最大でも2倍までしか増えません。一方、量子情報理論によると伝送される情報量を2倍以上に増やす、つまり C2 > 2C1と することが可能であると予言されています。この違いをもたらす要因は、信号を取り出す復号過程に量子力学の法則を取り込むか否かにあります。具体的には、 量子状態から信号を取り出す過程で、量子もつれを形成させながら測定を行うことで、古典情報理論の確率法則を超えた復号操作が可能になります。これは測定 を行う前に光の量子状態のままで量子計算を実行することに相当します。0,1,2を運ぶ光子の数をさらに増やして、一般にn個にすると情報量は C2 = nC1とさらに増えてゆきますが、増加の比率は一定値 ![]() へ収束してゆきます。これが最終的な伝送限界、いわゆる通信路容量になります。古典情報理論では、通信路容量は
へ収束してゆきます。これが最終的な伝送限界、いわゆる通信路容量になります。古典情報理論では、通信路容量は ![]() となります。
となります。
さて、まずは最も簡単な超加法的量子符号化利得 C2 > 2C1 を検証したいわけです。そのためには、2つの光子の間で量子計算ができなければななりません。しかし、それは現在の技術では、まだ難しく実際的ではありません。そこで、我々は光子数を倍に増やす代わりに、光子の空間自由度を倍に増やすことを考えました。通信資源は何も光子数だけではなく、空間帯域や周波数帯域も重要な通信資源になります。偏光とパルス位置の自由を使った信号フォーマットを用いるわけです。そして、空間帯域を倍に増やしたときに、送れる情報量が倍以上に増えるか否かを確認することになります。そうすると必要な符号化・復号化回路は比較的簡単な光学素子で構成できることになります。実際には、図8に示すような偏光干渉系と光子検出器から構成されます。
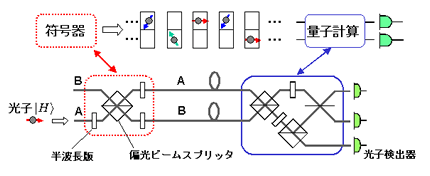
実際の回路構成を図9に示します。このような回路を光を遮断した空間に設置して、光子を1個1個その中へ導いて符号化・復号化の操作を行います。 APD0, APD1, APD2と書いている3つの光子検出器のどれに光子が出たかによって0, 1, 2のどれだったかを判定します。0, 1, 2のそれぞれについて平均10万回以上、符号化・復号化操作を実行して、その統計データから、伝送された情報量を評価します。
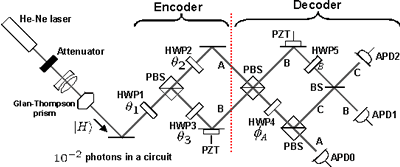
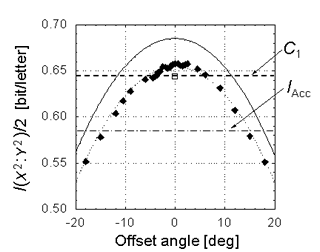
図10に、最終的な実験データを示します。縦軸が 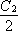 を表し、横軸のoffset angleとは、復号回路のあるパラメータ(信号ベクトルと測定ベクトルの相対角)を表しています。水平の破線が従来の限界 C1 の理論値で、黒の角印が実験データです。水平の破線の上に飛び出た部分が
を表し、横軸のoffset angleとは、復号回路のあるパラメータ(信号ベクトルと測定ベクトルの相対角)を表しています。水平の破線が従来の限界 C1 の理論値で、黒の角印が実験データです。水平の破線の上に飛び出た部分が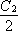 > C1 という超加法的量子符号化利得の実験的証拠になります。 2C1 = 1.2908 ビットを超えて C2 = 1.312 ± 0.005 ビットの情報が復号されたことが明確に示されています。実線が理論値です。実験値との差は、光学素子や回路の調整限界からくる不完全さのためです。このように、不確定性原理が支配する通信路では、量子計算を適切に用いた復号を行うことで、通信帯域の増加とともに取り出せる情報量を超加法的に増やせることが実証されました。
> C1 という超加法的量子符号化利得の実験的証拠になります。 2C1 = 1.2908 ビットを超えて C2 = 1.312 ± 0.005 ビットの情報が復号されたことが明確に示されています。実線が理論値です。実験値との差は、光学素子や回路の調整限界からくる不完全さのためです。このように、不確定性原理が支配する通信路では、量子計算を適切に用いた復号を行うことで、通信帯域の増加とともに取り出せる情報量を超加法的に増やせることが実証されました。
<文献情報>
M. Fujiwara, M. Takeoka, J. Mizuno and M. Sasaki,
"Exceeding classical capacity limit in quantum optical channel",
Phys. Rev. Lett., 90(16), 167906/1--4(2003).
M. Fujiwara, M. Takeoka, J. Mizuno and M. Sasaki,
"Exceeding classical capacity limit in quantum optical channel",
Phys. Rev. Lett., 90(16), 167906/1--4(2003).
佐々木雅英、武岡正裕、"量子通信路符号化",
応用物理学、Vol. 72, N0. 2, 169--175 (2003).
応用物理学、Vol. 72, N0. 2, 169--175 (2003).
M. Takeoka, M. Fujiwara, J. Mizuno, M. Sasaki,
"Implementation of generalized quantum measurements: Superadditive quantum coding, accessible information, and classical capacity limit",
Phys. Rev. A, 69(5) 052329-1--14 (2004).
"Implementation of generalized quantum measurements: Superadditive quantum coding, accessible information, and classical capacity limit",
Phys. Rev. A, 69(5) 052329-1--14 (2004).
意義
本研究成果は、量子力学と情報科学を結びつける上で、重要な基礎科学的意義を持っています。量子力学においては、古典力学にはない新しい現象として、量子 もつれという相関の重要性がその誕生当時の20世紀初頭からすでに認識されていました。一方、情報科学は、20世紀半ばにシャノンが通信路容量という概念 を導入して、通信理論を定式化することによって急速に発展しました。超加法的量子符号化利得は、この量子もつれ現象と通信路容量を結びつけることで初めて 生まれる概念です。この効果を実験的に検証するということは、20世紀に誕生した2つの基礎科学、量子力学と情報科学を融合してゆく上で、避けては通れな い通過点になります。我々の成果によって、量子もつれに対する新しい情報理論的意義が実験的に裏付けられ、同時に、通信路容量の量子力学的拡張の実験的基 礎も与えられたことになります。
一方、実用的には、情報需要の爆発的増加の中で、近い将来明確な性能限界に突き当たる従来の光通信技術にかわって、新しい通信の原理を示す成果として期待 されます。技術形態としては、信号を復号する際に量子計算の原理を使うもので、その核心的部分は受信側にあり、送信側では従来の光通信技術をそのまま生か す形態になります。その際、受信側で使う量子計算は少数のビットを扱う小規模のものでも、十分な技術的意義を持ちます。つまり、従来の復号回路の中に小規 模量子計算回路を組み込むことで、従来の通信性能を確実に改善してゆくことが可能です。これは、超高速計算技術として期待される量子計算が、本来、大きな 規模で動作させて初めてその威力を発揮できるのとは対照的で、量子計算の通信における新しい応用を示すものでもあります。この意味で、我々の成果は、従来 の光通信技術から最も自然な形で量子情報通信技術へ移行してゆく通過点に位置しているわけです。
今後の展開
今回の我々の実験では、光子の偏光と空間自由度を変調して信号を伝送しています。これは原理実証としては十分ですが、実際の伝送路では外乱に弱いため、実 用的にはあまり適していません。実際の通信に適した方式は、多くの光子が一つの波として束になったコヒーレント光と呼ばれる状態を変調する方式です。した がって、超加法的量子符号化利得も、いずれはコヒーレント光信号に対して実現する必要があります。しかし、残念ながらコヒーレント光信号の間で量子計算を 実行するのは、極めて難しい課題であり、多くの基盤技術が熟して初めて現実になる目標です。実用化にはまだまだ多くの基礎研究が必要なわけです。我々が最 初の原理実証として、光子の偏光と空間自由度を用いた理由は、これが現在の技術を使って最も正確な量子計算を実行できる唯一の物理系だからです。
今後の展開
今後は、コヒーレント光信号の間で量子計算を実行するための基礎研究に着手してゆきます。微弱なコヒーレント光信号での量子計算が可能になれば、1ビット 当たり平均1個に満たない光子のエネルギーでも、信頼性の高い情報伝送を実現することが倫理的に可能です。具体的には、2つの方向から研究に取り組んでゆ く計画です。1つの方向は、高精度の光子検出器と低雑音光源と高速の電子制御技術を組み合わせて量子計算を実行する方法です。この方法では処理速度はある 程度犠牲になりますが、5年程度で現在の技術を凌駕する最初の基本モデルを実現できると期待されます。もう1つの方向は、集積化が可能な固体化素子で光の 量子計算を実現する方向です。まずは、微弱な光信号に対しても大きな非線形効果を引き起こせる物理機構を探索してゆく必要があります。



